In the transportation industry, product reliability is critical, and many highly sensitive electronic products, medical equipment and specialized tools are often located thousands of miles away from the end user during the manufacturing process, and in order to deliver these items to customers, they must travel by road, rail, sea and air. These items are exposed to different types of vibration environments, so they need to arrive at their destination intact during transportation, which requires appropriate measures to be taken during transportation to ensure that these sensitive items can withstand the test of the vibration environment.

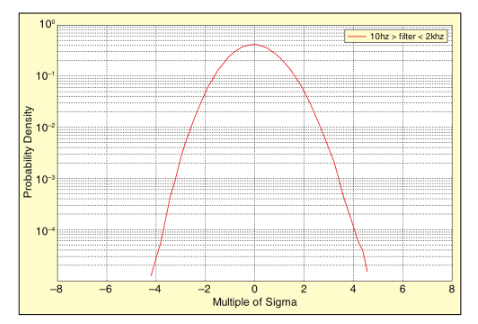
At present, the popular random vibration testing technology adopts Gaussian vibration method. For this purpose, the controller is designed to generate and maintain a bell-shaped signal probability density function (PDF), where the mean is zero and the normalized kurtosis value is 3. The spectral shape of this signal is controlled by feedback and has the expected root-mean-square density (sigma). By averaging the data, Gaussian control ensures that the maximum peak acceleration generated during the process does not exceed ±3sigma, or even less. (Refer to Figure 1, which shows that the kurtosis test acceleration is Gaussian). This method guarantees the stability and reliability in the process of vibration testing.
Subsequently, this testing process eliminated the very large acceleration spikes observed in the field data. While the Gaussian random vibration testing matched the raw field data in energy, the acceleration peaks were different. Therefore, the Gaussian random vibration test measurement method cannot be completely equivalent to the real vibration condition. It can be considered an incomplete test because it cannot simulate large acceleration values. In the transport industry, these Gaussian random vibration tests cannot replicate the large acceleration peaks seen in road, rail or air transport. Therefore, the packaging industry needs better packaging solutions to protect products.
Rather than using Gaussian random vibration for product testing, it is better to simulate field data more realistically by adjusting the probability distribution of excitation. This method requires adjusting the kurtosis parameter. Kurtosis is a statistical term used to describe the distribution of data. In simple terms, kurtosis describes the amount of peak acceleration in a data set. If you want more large peak accelerations in the test, you need to increase the kurtosis parameter. By increasing the kurtosis, a larger peak acceleration can be included without increasing the total energy of the test. This adjustment can more accurately simulate the real vibration scene and provide more realistic test results.
From Figure 2 we can observe that kurtosis is a measure of the size of the “tail” of the probability distribution. A dataset with a higher kurtosis value will present a distribution curve with a higher peak in the mean, along with a longer “tail”, or in other words, more data points at the extreme value. Compared to a traditional Gaussian distribution (a kurtosis value of 3), the distribution with a kurtosis value of 5.7 shown in Figure 2 has more data points in the “tail”, that is, data points that are far from the mean.
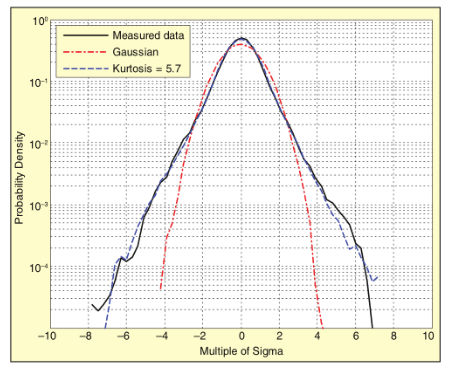
Note that kurtosis values contain a higher peak acceleration (±6 sigma) than Gaussian (±3 sigma). Also, note that kurtosis control distributions are more similar in real life measurements than Gaussian distributions.
For the transportation industry, the use of random vibration excitation with higher kurtosis value in vibration testing may be preferable to the Gaussian test excitation commonly used at present. Recent studies have shown that the vibration data in real life do not conform to the Gaussian distribution, but are closer to the distribution with higher kurtosis levels. Figure 2 shows how a distribution with a higher kurtosis is closer to the actual measured data than a Gaussian distribution. Therefore, random vibration excitation with a higher kurtosis value can more accurately simulate the real vibration situation and may be more suitable for the transportation industry.